Aufgrund des Buches Gravitation und Raumzeit - Die vierdimensionale Welt der Relativitätstheorie von John A. Wheeler führte ich vor einiger Zeit eine kurze PN-Diskussion mit Agent Scullie.
Nun habe ich mich entschlossen, über dieses Thema ein neuen Thread zu erstellen und den größten Teil meiner ersten PN für die Eröffnungspost zu verwenden. (Für Agent Scullie verweise ich auch auf Kapitel, Seiten und Excurse im Buch, damit er nicht alles selbst mühsam raussuchen muss. Lass euch davon bitte nicht irritieren.)
Besondere Verständisprobleme hatte ich beim Lesen Buches beim täuschend harmlosen Tiel "Steine im Flug und Planeten in Umlaufbahnen" (Kapitel 10).
Die Verständisprobleme sind übrigens in diesem Fall allein auf mich zurückzuführen. Wheelers Buch über die Realtivitätstheorie ist das beste populärwissenschaftliche Werk zum Thema, welches ich je gelesen hatte. (Es war ja auch eine Empfehlung von Agent Scullie, die ich nur weitergeben kann.) Es verbindet Anschaulichkeit und leichte Verständlichkeit mit Genauigkeit.
Die erste Frage bezieht sich auf den Begriff Radian (Exkurs 5.1 auf Seite 91).
Habe ich es so richtig im Sinn behalten, dass man als Radian ein möglichst kleines Kreissegment nimmt und es sich gewissermaßen um eine fast genaue "Annäherungsrechnung" an den tatsächlichen Wert handelt? Man nimmt also zwei "benachbarte" Punkte auf dem Kreis, verbindet sie durch eine gerade Linie, welche kaum von der tatsächlichen Bogenlänge abweicht und geht davon als die Bogenlänge aus?
Die zweite Frage bezieht sich auf das Bild auf Seite 137: Warum ist die obere Grafik, die die Schwarzschildmetrik eines Schwarzen Loches darstellt, wie der mathematische Plot eines Wurmloches ...

... und nicht so dargestellt?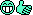

Meine dritte Frage bezieht sich auf das Kapitel 9 "Raum und Raumzeit in der Umgebung eines Massenzentrums", insbesondere auf "Exkurs 9.1. Genaugenommen verstehe ich die komplette Seite 165 leider nicht.
Bezeichnet die Schwarzschildradial-Koordinate r den Abstand von der "Achse" (die Ameise ist ein Stück nach oben gekrappelt) und die Winkelkoordinate d den Abstand vom benachbarten Punkt, also die Bogenlänge (die benachbarte Ameise in der Phalanx)?
Und m steht also für das geometrische Maß der Masse. Aber damit ist nicht der Schwarzschildradius gemeint, oder? Denn das geometrische Maß für ein schwarzes Loch mit 10 Sonnenmassen ist ja auch genau 10 mal so groß wie das der Sonne, also ein Längenmaß (Seiten 184 und 185).
Meine vorerst letzte Frage bezieht sich auf die radiale Bewegung und transversale Bewegung in Kapitel 10 (Seiten 178 und 179).
Verstehe ich es richtig, wenn ich annehme, dass die radiale Bewegung bei einer vollkommen kreisförmigen Bahn (nach Kopernikus) Null beträgt? Hat das nicht etwas mit den Radialkoordianten, also dem Abstand vom Gravitationszentrum, zu tun?
Dann wäre die Transversalbewegung also die Umlaufgeschwindigkeit, richtig?
BTW die Ameisen verwendete Wheeler zwecks Veranschaulichung. Sie krappeln in einer Phalanx die gekrümmte Fläche eines Porzellanparaboloids hoch und hinterlassen in gleichmäßigen Abständen rote Farbtupfer. Die gekrümmte Fläche veranschaulicht (um eine Dimension reduziert) die Raumkrümmung um ein kugelsymmetrisches Massezentrum (Schwarzschild-Lösung). Je weiter die Ameisen "nach oben" krappeln, je weiter entfernen sich die roten Makierungen voneinander. Verbindet man die Linien, auf denen die Ameisen gelaufen sind, erkennt man die relative Krümmung.
Die Ameisen könnten diese Krümmung ihrer 2-D-Welt ganz ohne dritte Dimension, anhand dieser relativen Krümmung anhand der Markierungen erkennen. Die gedachte Einbettungsdimension ist also überflüssig, um eine Raumkrümmung zu definieren und dient nur als geometrisches Hilfsmittel.
Der Porzellanparaboloid veranschaulicht mit seiner äußeren Krümmung also die innere Krümmung des Raumes. (Die Zeit wird hierbei erstmal vernachlässigt).
Nun habe ich mich entschlossen, über dieses Thema ein neuen Thread zu erstellen und den größten Teil meiner ersten PN für die Eröffnungspost zu verwenden. (Für Agent Scullie verweise ich auch auf Kapitel, Seiten und Excurse im Buch, damit er nicht alles selbst mühsam raussuchen muss. Lass euch davon bitte nicht irritieren.)
Besondere Verständisprobleme hatte ich beim Lesen Buches beim täuschend harmlosen Tiel "Steine im Flug und Planeten in Umlaufbahnen" (Kapitel 10).
Die Verständisprobleme sind übrigens in diesem Fall allein auf mich zurückzuführen. Wheelers Buch über die Realtivitätstheorie ist das beste populärwissenschaftliche Werk zum Thema, welches ich je gelesen hatte. (Es war ja auch eine Empfehlung von Agent Scullie, die ich nur weitergeben kann.) Es verbindet Anschaulichkeit und leichte Verständlichkeit mit Genauigkeit.
Die erste Frage bezieht sich auf den Begriff Radian (Exkurs 5.1 auf Seite 91).
Habe ich es so richtig im Sinn behalten, dass man als Radian ein möglichst kleines Kreissegment nimmt und es sich gewissermaßen um eine fast genaue "Annäherungsrechnung" an den tatsächlichen Wert handelt? Man nimmt also zwei "benachbarte" Punkte auf dem Kreis, verbindet sie durch eine gerade Linie, welche kaum von der tatsächlichen Bogenlänge abweicht und geht davon als die Bogenlänge aus?
Die zweite Frage bezieht sich auf das Bild auf Seite 137: Warum ist die obere Grafik, die die Schwarzschildmetrik eines Schwarzen Loches darstellt, wie der mathematische Plot eines Wurmloches ...

... und nicht so dargestellt?
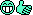

Meine dritte Frage bezieht sich auf das Kapitel 9 "Raum und Raumzeit in der Umgebung eines Massenzentrums", insbesondere auf "Exkurs 9.1. Genaugenommen verstehe ich die komplette Seite 165 leider nicht.

Bezeichnet die Schwarzschildradial-Koordinate r den Abstand von der "Achse" (die Ameise ist ein Stück nach oben gekrappelt) und die Winkelkoordinate d den Abstand vom benachbarten Punkt, also die Bogenlänge (die benachbarte Ameise in der Phalanx)?
Und m steht also für das geometrische Maß der Masse. Aber damit ist nicht der Schwarzschildradius gemeint, oder? Denn das geometrische Maß für ein schwarzes Loch mit 10 Sonnenmassen ist ja auch genau 10 mal so groß wie das der Sonne, also ein Längenmaß (Seiten 184 und 185).
Meine vorerst letzte Frage bezieht sich auf die radiale Bewegung und transversale Bewegung in Kapitel 10 (Seiten 178 und 179).
Verstehe ich es richtig, wenn ich annehme, dass die radiale Bewegung bei einer vollkommen kreisförmigen Bahn (nach Kopernikus) Null beträgt? Hat das nicht etwas mit den Radialkoordianten, also dem Abstand vom Gravitationszentrum, zu tun?
Dann wäre die Transversalbewegung also die Umlaufgeschwindigkeit, richtig?
BTW die Ameisen verwendete Wheeler zwecks Veranschaulichung. Sie krappeln in einer Phalanx die gekrümmte Fläche eines Porzellanparaboloids hoch und hinterlassen in gleichmäßigen Abständen rote Farbtupfer. Die gekrümmte Fläche veranschaulicht (um eine Dimension reduziert) die Raumkrümmung um ein kugelsymmetrisches Massezentrum (Schwarzschild-Lösung). Je weiter die Ameisen "nach oben" krappeln, je weiter entfernen sich die roten Makierungen voneinander. Verbindet man die Linien, auf denen die Ameisen gelaufen sind, erkennt man die relative Krümmung.
Die Ameisen könnten diese Krümmung ihrer 2-D-Welt ganz ohne dritte Dimension, anhand dieser relativen Krümmung anhand der Markierungen erkennen. Die gedachte Einbettungsdimension ist also überflüssig, um eine Raumkrümmung zu definieren und dient nur als geometrisches Hilfsmittel.
Der Porzellanparaboloid veranschaulicht mit seiner äußeren Krümmung also die innere Krümmung des Raumes. (Die Zeit wird hierbei erstmal vernachlässigt).



 ).
). ).
). Ich habe was begriffen.
Ich habe was begriffen. (Das schiebe ich mal auf den Konzentratinosmangel.)
(Das schiebe ich mal auf den Konzentratinosmangel.)

 Folgendes aus Wiki treffend ist
Folgendes aus Wiki treffend ist 
 und nicht in Quantenobjekten zerlegt werden will, muss ich ja nun hier wieder posten.
und nicht in Quantenobjekten zerlegt werden will, muss ich ja nun hier wieder posten.


Kommentar